寄稿 / 稲垣勝義氏
江戸時代には日本独特の数学が花開き、多くの庶民が興味を持って数学を学んだ歴史がある。江戸時代後期になると、全国各地に数学の愛好家が現れた。明治時代に入り、この江戸時代に発達した日本の数学を、ヨーロッパの数学(洋算)に対して「和算」と呼ぶようになった。日本には古くから神社に絵馬を奉納する習慣があるが、数学愛好家たちは和算の問題を解いて絵馬にして奉納した。この絵馬を「算額」と呼んでいる。三重県内にも多くの算額が残されており、それらを紹介しながら、和算とはどのようなものか記してみよう。
1 和算の歴史
和算は、古代中国の数学から基本を学んで作り上げた日本独特の数学である。16世紀末頃、『算法(さんぽう)統宗(とうそう)』、『算学(さんがく)啓蒙(けいもう)』などと称される中国の数学教科書が日本へ輸入されている。また、それ以前にも中国から輸入された教科書から、我々が小学校で学んだ、「九九」も学んでいた様子であり、その形跡は『万葉集』の歌の中にも見られる。一例を挙げると、「…朝猲(あさかりに) 十六履起之(ししふみおこし)…」(巻6・926)では十六は四×四であることから、しし(鹿猪)と読んでおり、「…夜(よる)哉将間(へだてむ) 二八十一(にくく)不在國(あらなくに) 」(巻11・2542)では、八十一は九×九であることから、二八十一をにくく、と読んでいる。
16世紀末頃にはソロバンも日本へもたらされて、広く普及し始めていた。ソロバンの教科書としては『割算書(わりざんしょ)』が元和8年(1622)に出版され、すぐ後の、寛永4年(1627)には、名著『塵劫記(じんこうき)』が出版された。この『塵劫記』は単なるソロバンの入門書ではなく、「米売り買いの事」「銀金両替の事」「万(よろず)利足の事」「検地の事」「川普請の事」など、当時の世の中で必要とされた農業、商業、土木などの数学が図も描かれ示されており、江戸時代の人々にとっては身近な数学の教科書であった。その後も次々と類似本が発行されて、江戸時代の人々の数学の知識水準は高くなった。明治になっても『明治塵劫記』が刊行されており、250年の長きにわたって出版が続いた超ロングセラーでもあった。
『塵劫記』以来、江戸時代の数学は中国数学の伝統を受け継ぎ、発展してきたが、内容的には今日の中学校の域であった。そのレベルを一気に引き上げたのが関 孝和(せき たかかず)(「孝和」は、「こうわ」とも読めるが、今日では「たかかず」が一般的である)であった。
2 関孝和の業績
関孝和は日本史の教科書にも名前が掲載されて、和算を語るうえでは欠かす事の出来ない人物であり、日本の数学の確立者であるといえる。関の没年は宝永5年(1708)であるが、その生涯は殆ど不明である。井原西鶴、松尾芭蕉らと同時代の人である。江戸時代の関以前の日本の数学レベルからみると、関が成し遂げた数学内容の質、業績は多大なものがあり、関以降の数学者へ大きな影響を与えた。
関の数学における業績のうち、代表的なものの1つは、記号代数の考案である。それまでは天元術といわれて、算木(長さ3~10センチの木製の直方体で並べることにより数を表す)を用いる方法であったため、未知数が1つで、係数が具体的な数値で与えられた方程式しか解くことが出来なかった。関はその形を紙の上に略記するとともに、傍らに文字を書き添える(傍書法とよばれている)ことによって、変数が2種類以上で、係数も文字記号で表すことにより、一般の整式の方程式も解くことが可能な方法を考えた。この方法で、方程式の計算が筆と紙を使って解く(いわゆる「筆算」)ことが可能になり、日本独自の数学が一挙に発展した。
また、円周率を3.1415 9265 35と11桁までの真値を計算で正しく求めたり、他にも行列式の算法の考案や、近似解法の考察など、数多くの理論を独自のアイデアで作り上げた人物である。
3 庶民の数学
江戸時代に多くの庶民が数学に興味を持ち、数学を学んでいるという現象はどこから来るのであろうか。その一つは年貢の上納制度である。年貢の請求は、村請制度と呼ばれ、藩から村役人である庄屋や名主のもとへ届くが、各戸への割り当ては村役人達の仕事であり、村役人達は税を徴収するために数学知識が不可欠であったことが要因として考えられる。また一方、この時代には商業活動も盛んになり、一般の人々にも歩合計算など、日常生活に数学知識の必要性が生じてきた。さらに、男女を問わず、寺子屋などで「読み書きそろばん」を学び、そろばんを用いて、暮らしに必要な初等的な数学を学んでいた。また同時に数学の塾も存在しており、数学の師匠に入門して、数学を楽しみとする愛好者たちもいたのである。余談であるが、島崎藤村の名著「夜明け前」の文中でも、木曽馬籠宿の当主、青山吉左衛門が和算を学んだことが書かれている。
江戸時代における、数学に関わった人々を大雑把に分けると、
① ソロバンなど日常生活に必要なアイテムとして数学を使っていた人々
② 単なる日用数学を超えて、師匠に入門して教えを乞う人々
すなわち、趣味の感覚で数学を楽しんでいた人々である。彼らは、数学自体に興味、関心を持ち、平面幾何や立体幾何などの問題を中心にして、日常生活とは無縁な数学の問題を考え、互いに問題を出しあったり、自分の解いた問題を絵馬にして神社に掲げたりして、俳句や書画と同じ感覚で数学を楽しんでいた人々である。
③ 和算としての数学的な業績を残した人々
いわゆる数学の師匠クラスの人々である。これらの人々は数学の教科書を出版したり、新しい発想で解法の開発を企てたりした。和算の数学的業績を歴史に名を残した人々である。
いずれにせよ、江戸時代の和算の世界には、身分制度、男女の枠を超えた、数学の世界をそれぞれに楽しむ、自由な空間が存在していたのである。
4 文化としての算額

神社仏閣に算額奉納の習慣がいつから始まったのかは定かでない。当時数学を学ぶ者として、数学の難問が解けたことを神に感謝する意味のほかに、自分の研究発表の場として、問題を広く世に知らせる意味も含まれていたのかも知れない。和算を学ぶ者達にとって、算額を奉納することは一つの目標であり、夢であったに違いない。
和算を学ぶ者達には「遺題承継」といった習慣がある。問題を解いた者が、新しい問題に解答を付けずに提出し、それを見た他の数学者が問題を解き、それに答えた算額に、また解答を付けないで新しい問題を出題するという習慣である。これを次々に承け継いでいくのであるが、問題を提出する者はそれ以上の難問を提出しなければならず、徐々に難しくなっていった。この事も、数学が進歩した要因の一つと考えられる。
現在、中部地方で確認されている算額の枚数は、愛知県63枚(16枚)、岐阜県25枚(8枚)、三重県30枚(11枚)と言われている(かっこ内は現存枚数)。
5 身近な算額
三重県でも算額が発見されており、和算の愛好者が多くいたことが伺える。ここでは、四日市市川島町の神明神社の算額を紹介しよう。昭和53年(1983)に発見され、寛政2年(1790)、天保15年(1844)、文久3年(1863)に奉納された2枚の算額が現存している。また、この神社から6~15キロ以内にある菰野町地内の神社でも算額が発見されており、同じ師匠に数学を学んでいたという可能性も指摘されている。この辺り一帯は数学の盛んな地域であったのかもの知れない。同時期に、鈴鹿の山を越えた近江(滋賀県)の神社にも同様の算額が掲載されていて、同じ問題を解いていた可能性も指摘されており、鈴鹿の山を越えた東近江との地域的な繋がりも考えられて、興味深いところである。これらの事からも数学の問題を解くことが当時の人々の間に、文化として数学が広がっていた事がしのばれる。
算額を奉納した、柳川安左衛門は神明神社の氏子と思われるが、先生の石垣宇左衛門は武州忍藩の人であり、現在の埼玉県行田市にあった藩である。当時の三重県北勢地域は他藩の飛地(分散している領地)が多く、他領が入り組んでいた地域で、忍藩の陣屋(藩の代官の住居、役所が置かれた建物)は、現在の大矢知興譲小学校の場所に置かれていた。忍藩藩士の石垣宇左衛門は勘定方を勤めていた者であり、数学にも長けていたと思われる。安左衛門は石垣先生の所へ、川島村から大矢知村まで、約8~9キロの道のりを歩いて教えを請いに通っていたことになる。
6 和算の衰退と西洋数学の流入
偉大な数学者、関孝和らによって、和算は18世紀に大きな進歩があった。関は「数学とは何のためのものかと言えば、難問、易問全てを解いて明らかにする術を学ぶためのものである」と述べている。
われわれが「和算」のイメージでまず頭に浮かぶのは、「幾何図形の諸問題」であるが、そこには、日本人の図形に対する美的感覚がバックボーンにあるように思われる。図形そのものに対する日本的な美を見出していたのである。さらに、華道や書道と同じように、和算家には芸道としての数学があった。また、遺題継承の習慣によって、幾何の問題を無尽蔵に生み出すことが出来たことも影響している。その上、問題解法のための複雑な計算技能力、問題に対する洞察力が日本の伝統数学の大きな推進力になっていた。それらの事柄が、250年以上も日本独特の数学文化が継承できた所以である。
だが一方、見た目の美しさや複雑さに入り込み過ぎ、数学的な本質から離れて行ってしまったため、それ以上に数学の範囲は広まらなかった。18世紀後半には、天文、航海術、三角関数表、対数表などの西洋の数学が断片的に日本へも入り始めているが、もともと、日本文化の中での和算の位置づけは、一部の和算研究家を除き、数学愛好家たちや、旦那衆の趣
味の世界のものであり、その趣味の世界からは出ることが出来なかったのである。
それに対して、西洋数学は物体の落体研究などを通じて、自然界の様々な現象に数学的な解析を用いたり、戦争が勃発した際には、大砲の弾道軌道計算などに数理的解法を考えることによって、新しい数学が生まれて数学の拡大範囲が広まっていった。
日本では江戸末期になって、浦賀に黒船が押し寄せてきた際、和算が軍事面に応用できない事が明白になり和算の限界が意識され始めた。安政2年(1855)江戸幕府は長崎に長崎海軍伝習所を開設して、オランダ人教師から操船術などを学び、海軍の士官を養成しようとした。そこでは、西洋数学の講義もあり、微積分学も教えられていたのである。
その後、江戸幕府が崩壊し、1868年には明治政府が発足したが、新政府の役割は、西洋に対抗しうる国家の樹立であり、そのためには富国強兵を実現しなければならなかった。そのため、新しい教育制度においては、西洋数学の採用が決定された。発足当初は和算家が初等数学教育を支えたが、そのうちに海外に派遣された若い留学生が西洋数学を学んで帰国し、新しい数学教育の指導者になるに及んで、17世紀以来の日本独特の素晴らしい「和算文化」は実質的に終わってしまったのである。
7 おわりに
江戸時代に栄えた「和算」は日本人独自の感性により、大きな発展を遂げ、独自の数学の世界を繰り広げた。その数学は、現代の中高校生の受験数学ではなく、問題に興味を持ったものが楽しみながら、ゆとりをもって問題を考え、互いに問題を出し合ったりして解く数学であった。彼らは、師匠や先輩、あるいは書物から学んだ後、自分で問題を作成し、仲間や師匠に見せるのを楽しみ、また、神社に算額として奉納することを誇りとした。
現代において受験数学では、先ず公式を覚え、次に答えのある問題を、公式を適用して解くゲームであると考えられなくもない (学校の先生によっては、数学は暗記だと極論を述べる先生もいらっしゃるようだが……)。そこで現在、その日暮らしの隠居生活を送っている筆者は、江戸時代の人々が俳諧や書画などの趣味を楽しんだように、和算の問題を時間に縛られずに解きながら、楽しい老後を過ごしたいと考えている。
島神明神社に奉納された算額の中の問題の2題を現代語訳して紹介してみよう。
闡微(ひらび)算法(さんぽう)一十五條第一答
いま、28種類の香が図のように環形にある。初日に(角)を嗅いで、二日に(氐)、三日に(尾)、四日に(女)をというように逐次この薫りを嗅ぐ。客が言うには、箕木は名香といわれる。他日に来てこの箕木の香りを嗅ぐには何日後にここに来たらよいかと。
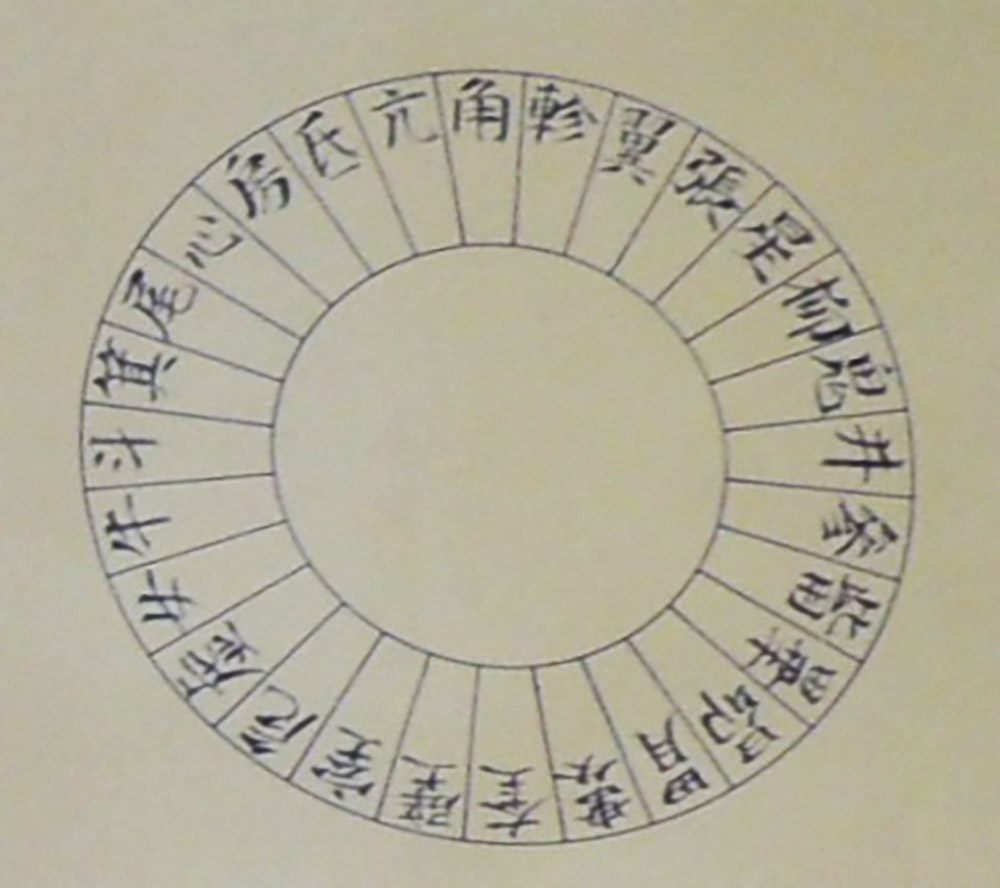
頭に”闡微(ひらび)算法(さんぽう)“とあるのは、寛延3年(1750)に表わされた『闡微算法』に遺題として掲載された15問の内の1つの答であるという意味である。この問題は、前述の『塵劫記』の中の「継子立て」と言われる類の問題である。嗅いだ香木は順次取り除いていくのが一般的であるが、ここでは問題の条件を変更して、嗅いだ香木を取り除かないで回答されている。(図1)のように、輪に並べた香木の匂いを嗅いで規則に従って(角→?→尾→女→……)次々に嗅いでいき、指定した香木(箕)を嗅ぐのは何日目か。という問題であるが、現代の高校生なら数列を利用して解く問題であるが、中学生でも数学が得意な人は解くことが出来るかもしれない。
天保15年(1844年)に奉納された算額(難問!)
今、図のように累円と挟円を描く、大円の直径は121寸8分、末円の直径は1分である。初円より末円に至るまでの円の総計を問う。
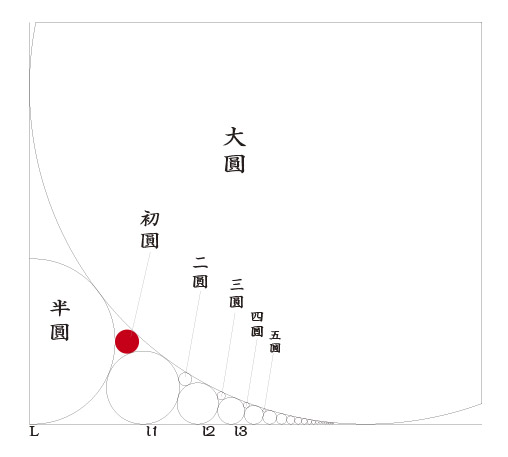
答 16個
計算法 大円の直径を末円の直径の四倍したもので割って、平方に開き、一を引いて円の個数として、問題の条件に合う。
武州忍藩 石垣宇左衛門知義門人
願主 柳川安左衛門
問題の題意は、(図2)のような、大円の直径が121.8寸(※これは122.8寸の誤記と思われる)、末円の直径が0.1寸のとき、初円から末円まで何個あるか、という問いである。答は16個となっており、計算法として、大円の直径を末円の直径の4倍したもので割って平方に開き1を引いて円の個数とするという事だが、数式で表すと、大円の直径をR、末円の直径をrとするとき[√(R/4r)]-1である(ここで記号[ ]は、小数点以下を捨てる記号である)。問題そのものも難しいが、この算額の裏面に柳川安左衛門の門人が解説を書いていることも興味をひかれる。
【参考文献】
◆小倉 金之助『日本の数学』岩波新書(1998) ◆平山 諦『和算の歴史』ちくま学芸文庫(2007)平山 諦『和算史上の人々』ちくま学芸文庫(2008) ◆小川 束『和算』中公選書(2021) ◆上野 健爾『和算への誘い 数学を楽しんだ江戸時代』平凡社(2017) ◆村田 全『日本の数学西洋の数学』中公新書(1981) ◆深川 英俊、ダン・ペドー共著『日本の幾何―何題解けますか?』森北出版株式会社(1994)











